こんにちは。初めまして。レッジのインターン生の大熊です。 レッジでは、ダッシュボードの作成や工場設備の異常検知など、データ利活用に関わる業務に取り組んでいます。
今回の記事では、最近少し話題になったマルチエージェントシミュレーションについて書いていきます。
コロナの影響から、感染症の拡大に関する様々な研究を目にする機会が増えました。その中でマルチエージェントシミュレーションという手法を利用して感染症拡大の様子を再現しているものが散見され、気になって調べてみました。
一般的な予測分析の場合、マクロデータをダイレクトに予測します。その一方でマルチエージェントベースの予測の場合、ミクロデータの相互作用からマクロデータを表します。現在は交通分野や防災分野での活用が進んでいますが、ビジネスサイドにおける活用も今後期待できそうな手法です。
本稿では、「マルチエージェントって言葉はなんとなく聞いたことがあるけれど、いまいちよくわかっていない」という方に向けて、その概要・適用例・Pythonを使用した簡単な実装例をご紹介します。
マルチエージェントシミュレーション（MAS）とは
マルチエージェントシミュレーションの「マルチエージェント」とは、「複数のエージェントが存在し、相互に影響しあう環境」のことを指します。
ここでいうエージェントとは、自律的な行動基準を持って行動し、周囲の環境に影響を与えるような人やモノのことを言います。具体的には、エージェントは以下の3つの特徴を持ちます。
- 自律性：エージェントが自身の行動指針に従って行動する
- 反応性：周囲の状況から、自身の行動を変化させる
- 社会性：周囲と依存的な関係にあり、相互作用を生む
マルチエージェントの枠組みでは、こうした特徴を持つエージェントが一つ一つが互いに影響しあい、全体の現象を作り出すこと（創発）に注目します。
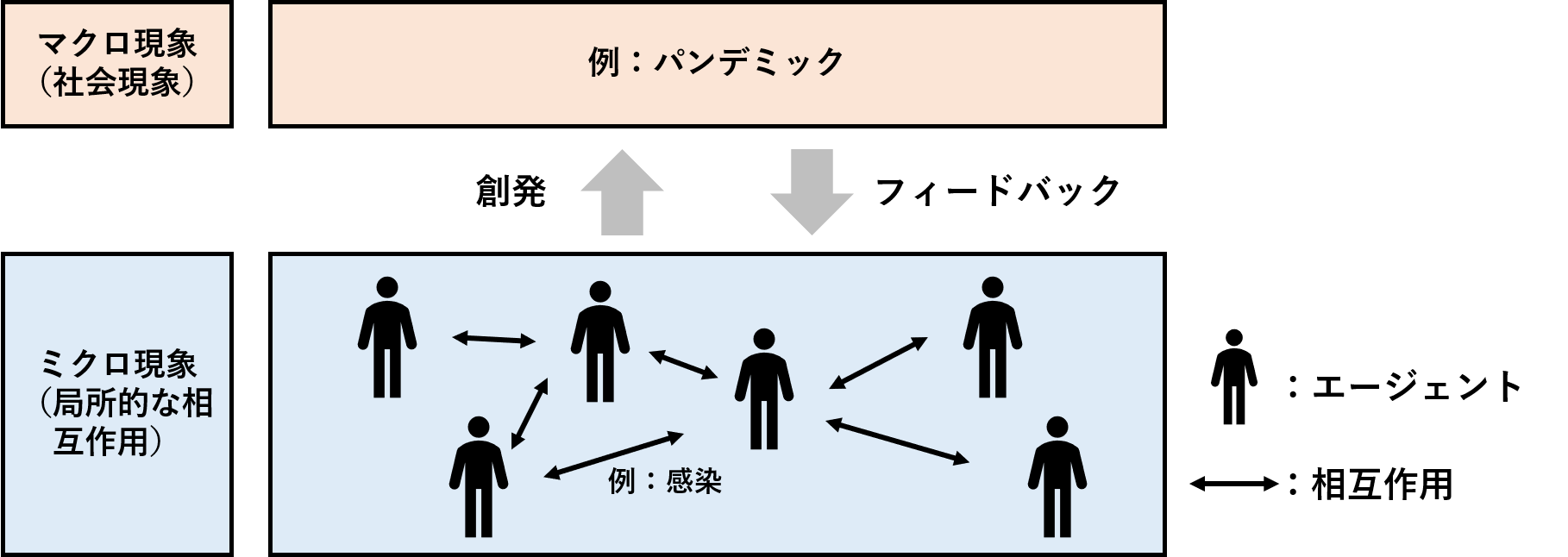
この創発の例として、ゴールデンウィークやお盆休み時の交通渋滞が挙げられます。帰省や旅行など、車を運転する目的（＝ミクロ的要因）は個人によってそれぞれ異なります。しかしそうした個人の運転を俯瞰的にみて交通状況全体を観察すると、交通渋滞というマクロ的な現象が形成されます。
MASでは、コンピュータの中に仮想世界（人工社会）を用意し、その中にエージェントを複数配置します。そしてそのエージェントたちは相互作用を繰り返します。その相互作用の結果として仮想世界全体に生じたマクロな現象やその現象が生まれるプロセスをMASでは確認することができます。
言い換えると、MASを用いることで、前提として置いたシンプルな仮定（＝個人の運転）から、それらの積み上がりによって生まれるダイナミックで複雑な現象（＝交通渋滞）を観測することができるようになります。こうした特徴から、大勢の人間や動物などの集団がどのように挙動していくのかを目的にMASは使用されます。
一般的なシミュレーションモデルとMASの違い
一般的なシミュレーションでは現象全体をモデル化するのに対して、MASでは現象の構成要素を個別にモデル化して全体の現象を観測します。
例えば、ある商品Aの売上を予測するとします。一般的な方法では、その売上の時系列的な変化や、売上と相関関係にありそうな変数（広告出稿数や気温など）に着目して、売上変化を表す微分方程式などの方程式を立てます。その方程式を解くことで予測値を求め、実際の現象を理解します。
その一方でMASでは、まずエージェントの行動パターンを定めます。例えば使用する行動パターンが過去の購買行動と周囲のエージェントの行動（例：口コミとか）に依存する場合、各エージェントごとに過去の購買行動と周囲の状況から商品Aを購買するかどうかを決定します。そして、そのエージェントたちの購買の全体の結果として、商品Aの売上金額が予測されることになります。
また マルチエージェントシステムのスタンスとして、エージェントの行動規範は簡潔にモデル化されるところが特徴です。 実際には複雑に見える社会現象でも、個々の行動に着目すれば意外とシンプルなことはよく見られます。 このような違いから、経済・社会活動において必要な変数や実例が大量に必要で全体をモデリングすることが難しい場合、MASは、比較的簡潔に現象の構成要素をモデル化でき、かつそうした社会現象を仮想空間内で再現できる点で有用な手法になります。
| 通常のシミュレーションモデル | マルチエージェント・シミュレーションモデル | |
|---|---|---|
| 内容 | 現象全体を記述する支配方程式を想定し、そうした支配方程式による現象のモデル化を行い、シミュレーションを実行する | 個々のエージェントの行動するルールを記述し、それらエージェント同士の相互作用によって全体としてどのような現象が現れてくるかに注目する |
| 対象 | 現象全体をモデル化 | 現象の構成要素（エージェント）1つひとつをモデル化 |
| 視点 | 外部から見ている観察者の視点 | 現象の構成要素（エージェント） |
| 特記事項 | 状態量の変化を観察（例、T期とT+1期の比較） | 個々のエージェントは、T期といった意識はない。自分の処理の順番で、自分のルールに則って処理を行う。その結果が、外部の観察者にはT期の現象として見える |
| 有効な場面 | マクロな現象のみを対象に説明・予測を行いたい場合。 | 個人行動の相互作用に着目し、個人レベルのミクロな現象をマクロな現象と結び付けたい場合。個人レベルに関するデータがある、もしくは個人レベルの行動をルール化できる場合。（例：感染症拡大、交通渋滞、店舗内回遊分析、など） |
（出所：北中英明（2005）『複雑系マーケティング入門ーマルチエージェント・シミュレーションによるマーケティングー』共立出版）
マルチエージェントシミュレーションの適用例
マルチエージェントシミュレーションは交通分野や防災分野でよく用いられている手法です。しかし近年のデジタル化を背景にミクロレベルのデータを取れるようになったことから、様々な分野での適用例が見られています。本章ではMASを活用した3つの研究ご紹介いたします。
例1：マーケティングにおける適用例
各エージェントを消費者と見立てると、消費者の購買行動が企業にもたらす影響もMASによって把握することができます。仮想空間上に消費者エージェントを配置し、各エージェントに購買行動させ、その購買行動の結果を調査することで、消費者単位の購買行動と企業への影響を確認することができます。
例えば岸本他(2009)は、店舗内のレイアウトと顧客の店舗内移動距離（＝動線長という）の関係をMASでモデル化して分析しています。この場合、店舗に訪れる顧客がエージェントとなり、各エージェントは予算や歩行速度、計画購買点数などのパラメータを与えられているほか、「計画購買商品売り場以外でも商品を見て回る」、「最も顧客エージェントが少ないレジに並ぶ」、などの店舗内での行動ルールを持っています。シミュレーションの結果、レイアウトの変更によって動線長に変化があることがわかっています。特に野菜/果物の売り場の配置を店舗奥に配置することが効果的であることが示されています。
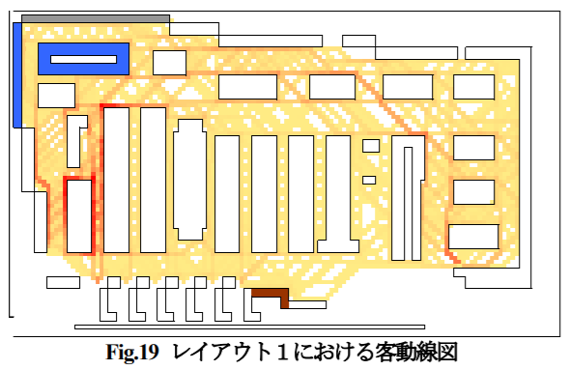（出所：岸本有之（2009）『エージェントシミュレーションによる小売店舗内商品販売促進施策の分析』）
例2：避難シミュレーションにおける適用例
MASが個々に自律的な行動規範を持ったエージェントを使用して仮想空間でシミュレーションを行うことから、現実世界では再現が難しい災害時における避難のシミュレーションにMASはよく用いられています。
具体的な適用例として、中島他(2018)は松山城を題材にしてMASを用いた避難シミュレーションを行ってます。その研究では、避難誘導の時に出口が複数あるとき、被害を最小化するためにそれら出口に対してどの程度誘導すべきか、というのを目的に分析を行っています。各エージェント（来訪者）には建物内の初期位置と歩行速度が設定され、その位置から最も近い避難先に移動するようにモデル化されています。このアルゴリズムを持ったエージェントを使用して、階段Aが最寄のエージェントの一定割合を階段Bに誘導することで避難完了時間に変化が出るのかを検証しています。シミュレーションの結果、誘導割合を56~60%に設定して避難計画を立案することが最も望ましいということが示されています。
（出所：中島昌暉・山田悟史（2018）『松山城における非合理的避難の割合と被害の推移に関する研究―マルチエージェントを用いた避難シミュレーション―』）
例3：デマの拡散のシミュレーション（マルチエージェントによるマルチバースト型デマ拡散モデルの構築）
情報拡散や感染症の拡大をシミュレートする際にも、MASは用いられることがあります。
池田他(2016)はTwitter上のユーザーをエージェントとして、Twitterでデマが流れるときのシミュレーションを行っています。Twitterのユーザーはほかのユーザーから情報を受け取り、内容に興味があれば関連する内容を新たにツイートします。この例では「情報を何も受け取っていないエージェント」、「デマ情報を受け取ったエージェント」、「デマ情報を投稿したエージェント」、「訂正情報を受け取ったエージェント」、「訂正情報を投稿したエージェント」の5つのエージェントを用意して、各エージェントには「影響度」、「興味度」、「感度」のパラメータを与えています。これにより各ユーザーが情報を複数回受け取る状況を再現できるようにしています。こうした属性を持つ複数のエージェントをスケールフリーネットワークと呼ばれるネットワーク構造の中に配置することで、エージェント同士の相互作用の再現し、デマの拡散のされ方をシミュレーションしています。
感染症拡大をテーマにした簡単なMASの実装例
最後にMASの挙動を確認するため、簡単なMASの実装を行ってみます。エージェントの相互作用のイメージが「感染」という形で理解しやすい、感染症拡大の可視化をテーマに実装を行います。可視化のレイアウトはこちらを参考にさせていただきました。
また今回の実装はMASの挙動を理解することが目的なので、MAS用の特別なライブラリを用いずに、Python標準ライブラリで実装します。（シミュレーションの可視化ではmatplotlibを使用します）コードはこちらに上げてあります。
【各エージェントのルール説明】
今回はある空間を用意してそこにエージェントをランダムに配置していきます。 感染症の拡大を予測する伝統的なモデルであるSIR(Susceptible, Infectious, or Recovered)モデル に則り、各エージェントには以下の属性を与えます。また感染症対策として➀マスク着用の有無、②自粛の有無という属性が付加されています。
各エージェントの行動のルールは以下のように定めます
以上のルールのもと、エージェントを空間内に動き回らせ、エージェント同士の相互作用によってどのように感染が拡大していくのかを確認します。なお今回の実装では、「時間の経過によってエージェントが学習し、行動が変化する」、ということは考慮しないこととします。
➀感染症対策なしの場合vs自粛行動ありの場合
まず、エージェントが活動を制限することで感染拡大がどのように変化するのかを見ていきます。左側が何もしない場合、右側が自粛をし行動を制限した場合を表しています。右側では8割のエージェントが行動を自粛しています。 そして下段の積み上げエリアグラフは、各健康状態のエージェントがどの程度いるのかを表しています。 また、青：健常者、赤：感染者、緑：免疫獲得者、黒：死亡者を示してます。
左側のように何も対策を行わないと急激に感染者が増加することがわかります。その一方で行動を制限すると、感染者数がなだらかに増減することわかります。
➁感染症対策なしの場合vs一部マスクありの場合
次に、感染者がマスクをすることで染拡大がどのように変化するのかを見ていきます。左側が何もしない場合、右側がマスクを積極的に着用している場合を表しています。右側では8割のエージェントが行動を自粛しています。 ➀と同様、下段の積み上げエリアグラフは、各健康状態のエージェントがどの程度いるのかを表しており、青：健常者、赤：感染者、緑：免疫獲得者、黒：死亡者を示してます。
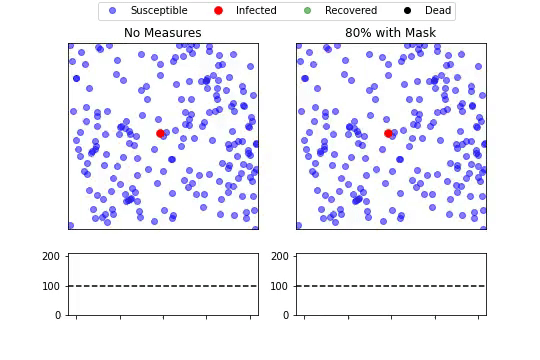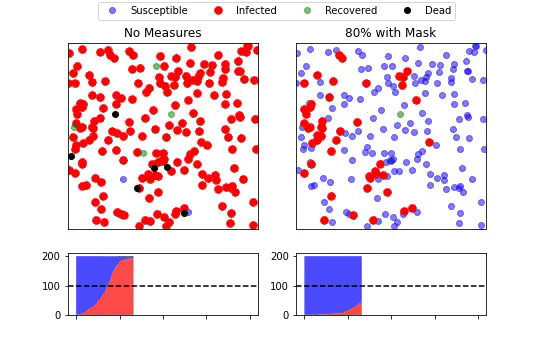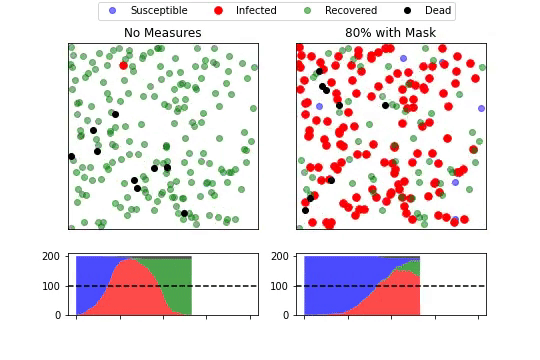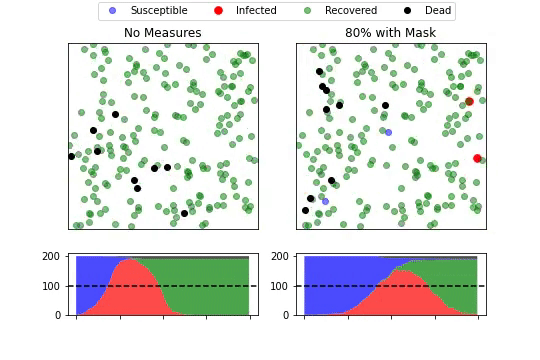
何もしない左側に比べて、マスクを着用している右側ではピークが遅れていることがわかります。しかしピーク時の山の高さは自粛時の比べかなり高くなっています。やはり行動を控えなければ、感染拡大を防ぐのは難しいと言えそうです。
以上、感染症拡大を例にMASを実装してみました。 現実世界をかなり簡略化しているので、モデルの妥当性は要検討ですが、シンプルなエージェントの仮定、エージェント同士の相互作用から全体として感染症が拡大していく様子が見て取れたかと思います。
最後に
本稿ではMASの概要から適用例、簡単な実装までをご紹介しました。 個人レベルのデータがあって個人行動をモデリングできる時、有効な手法になりそうです。シンプルな前提を置いているのに複雑な現象を記述できるため、オンラインサービスの普及やID-POSデータの活用、店内の導線データなど、粒度の細かいデータの活用が進んでいる現在において、MASはその妥当性が認められてくる手法だと思います。強化学習との相性も非常に良いので、よりビジネスサイドでの今後の活用が期待されるのではないでしょうか。
参考資料
- 小高知宏（2018）『Pythonによる数値計算とシミュレーション』オーム社
- 北中英明（2005）『複雑系マーケティング入門ーマルチエージェント・シミュレーションによるマーケティングー』共立出版
- 和泉潔・斎藤正也・山田健太（2017）『マルチエージェントのためのデータ解析』（コロナ社）
- 丸井義章（2010）『スタミナを考慮した避難シミュレーション』
- 藤長愛一郎ら（2014）『動的解析手法を用いたインフルエンザ対策の検討』
- 金月寛彰ら（2018）『マルチエージェントシミュレーションによるタクシー営業戦略の改善シナリオの提案』
- 岸本有之（2009）『エージェントシミュレーションによる小売店舗内商品販売促進施策の分析』
- 坪井一晃ら（2015）『ACO型時系列パターン抽出法を用いたマーケティングデータの考察』
- 中島昌暉・山田悟史（2018）『松山城における非合理的避難の割合と被害の推移に関する研究―マルチエージェントを用いた避難シミュレーション―』
（参考）実装コード
※Google colabratory上で実行しています。
import math import random import copy import matplotlib.pyplot as plt from matplotlib import animation, rc, gridspec from IPython.display import HTML N = 200 # エージェントの個数 SIZE = N # 仮想空間のサイズ TIMELIMIT = 200 # シミュレーションの打ち切り時刻 SEED = 65535 # 乱数の初期化 R = 15 # 感染範囲 SPEED = N/50 # エージェントの歩幅 TREATMENT_PERIOD = 60 # 感染してから治るまでの期間 MORTALITY_RATE = 0.05 # 死亡率 MORTALITY_PERIOD = 20 # 感染から死亡までの期間 CONTROL_RATE = 0.8 # 自粛する割合（0～1） CONTROL_RATE_AFTER = 0.0 # 対策後に自粛する割合（0～1） MASK_RATE = 0.0 # マスクを装着している割合（0～1） OVER_CAPACITY = N/2 # 感染拡大の目安 REQUEST_NOT_TO_GO_OUTSIDE_F = False # 途中で自粛命令を出すか否か #Agent class class Agent: """ エージェントを表現するクラスの定義 Attributes ---------- state : string エージェントの健康状態。S(健常状態), I(感染), R(免疫獲得), D(死亡)。 x : int エージェントのx座標。 y : int エージェントのy座標。 x_v : float エージェントのx座標方向の速度。 y_v : float エージェントのy座標方向の速度。 term : int 感染してからの日数。 mask : int(0 or 1) マスク着用の有無。0はマスクなしで1はマスクあり。 control_f : int(0 or 1) 活動自粛の有無。0は自粛（移動スピードが小さい）、1は普段通り行動。 mortality : int(0 or 1) 感染した場合生き残れるかどうかのID。 """ def __init__(self, state): self.state = state # 状態の設定（S or I or R or D） self.x = random.randint(1,SIZE) # x座標の初期値 self.y = random.randint(1,SIZE) # y座標の初期値 radian = math.radians(random.randint(1,360)) self.x_v = math.cos(radian)*SPEED # x方向の速さ self.y_v = math.sin(radian)*SPEED # y方向の速さ self.term = 0 # 感染してからの日数 self.mask_f = 0 # マスク着用の有無 self.control_f = 1 # 活動自粛の有無 self.mortality = random.random() # 感染した場合生き残れるかどうかのID def _calcnext(self, agents): # 次時刻の計算 if self.state == "S": self._state_S(agents) # 状態S用の計算 elif self.state == "I": self._state_I() # 状態I用の計算 elif self.state == "R": self._state_R() # 状態R用の計算 elif self.state == "D": self._state_D() # 状態D用の計算 else: # 合致するカテゴリがない print("ERROR カテゴリがありません") def _update_xy(self): """ エージェントのxy座標を更新する """ if self.x + self.x_v < 0 or SIZE < self.x + self.x_v: self.x_v *= -1 if self.y + self.y_v < 0 or SIZE < self.y + self.y_v: self.y_v *= -1 self.x = self.x + self.x_v * self.control_f self.y = self.y + self.y_v * self.control_f def _state_S(self, agents): # 状態Sの計算メソッド # カテゴリ1のすべてのエージェントとの距離を調べる sx = self.x # 状態Sのx座標 sy = self.y # 状態Sのy座標 for i in range(len(agents)): ax = agents[i].x # 抽出したstate1のx座標 ay = agents[i].y # 抽出したstate1のx座標 if agents[i].mask_f == 1: # マスクの有無による感染範囲の設定 aR = R/4 else: aR = R if agents[i].state == "I": if (sx-ax)*(sx-ax) + (sy-ay)*(sy-ay) < aR: # 指定した範囲内に状態Iがいる場合 self.state = "I" # 状態Iに変換（感染） self.term += 1 # 感染日数に1を追加する break # xy座標を更新 self._update_xy() def _state_I(self): # 状態Iの計算メソッド self.term += 1 # 感染日数を追加 if self.term > TREATMENT_PERIOD: # 一定の感染日数が経つと免疫を獲得する self.state = "R" if self.term > MORTALITY_PERIOD and self.mortality < MORTALITY_RATE: self.state = "D" # xy座標を更新 self._update_xy() def _state_R(self): # 状態Rの計算メソッド # xy座標を更新 self._update_xy() def _state_D(self): pass # agentクラスの定義終わり def calcn(agents): """次時刻の状態を計算""" # 状態Sのデータ xlistS, ylistS = [], [] # 状態Iのデータ xlistI, ylistI = [], [] # 状態Rのデータ xlistR, ylistR = [], [] # 状態Dのデータ xlistD, ylistD = [], [] for i in range(len(agents)): agents[i]._calcnext(agents) # a[i].putstate() # グラフデータに現在位置を追加 if agents[i].state == "S": xlistS.append(agents[i].x) ylistS.append(agents[i].y) elif agents[i].state == "I": xlistI.append(agents[i].x) ylistI.append(agents[i].y) elif agents[i].state == "R": xlistR.append(agents[i].x) ylistR.append(agents[i].y) elif agents[i].state == "D": xlistD.append(agents[i].x) ylistD.append(agents[i].y) return xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD # calcn()関数の終わり def scatter_plot(image, n, xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD): """散布図描画用関数""" image += ax[n].plot(xlistS, ylistS, ".", markersize=12, label="Susceptible", color="b", alpha=0.5) #状態Sのプロット image += ax[n].plot(xlistI, ylistI, ".", markersize=15, label="Infected", color="r") #状態Iのプロット image += ax[n].plot(xlistR, ylistR, ".", markersize=12, label="Recovered", color="g", alpha=0.5) #状態Rのプロット image += ax[n].plot(xlistD, ylistD, ".", markersize=12, label="Dead", color="k") #状態Dのプロット return image # 初期化 random.seed(SEED) # 乱数の初期化 # 状態SのエージェントをN個生成 agentsA = [Agent("S") for i in range(N)] # 対策あり可視化用エージェントを複製 agentsB = copy.deepcopy(agentsA) # 自粛するエージェントの設定 for agent in random.sample(agentsB,int(CONTROL_RATE*N)): agent.control_f = 0 # マスクを着用するエージェントの設定 for agent in random.sample(agentsB,int(MASK_RATE*N)): agent.mask_f = 1 # 状態Iのエージェントの設定 agentsA[0].state = "I" agentsA[0].x = SIZE/2 agentsA[0].y = SIZE/2 agentsA[0].control_f = 1 agentsB[0].state = "I" agentsB[0].x = SIZE/2 agentsB[0].y = SIZE/2 agentsB[0].control_f = 1 # グラフデータの初期化 T = [] # Statas数推移 statasS_sum_left= [] statasI_sum_left= [] statasR_sum_left= [] statasD_sum_left= [] statasS_sum_right= [] statasI_sum_right= [] statasR_sum_right= [] statasD_sum_right= [] #描画するグラフの設定 fig = plt.figure(figsize=(7.5,5)) gs = gridspec.GridSpec(2, 2, height_ratios=(3, 1)) ax = [plt.subplot(gs[0, 0]), plt.subplot(gs[0, 1]), plt.subplot(gs[1, 0]), plt.subplot(gs[1, 1])] #空のグラフが出てしまうのを回避 plt.close() #アニメーション用のグラフ保管場所 ims = [] legend_flag = True # 凡例描画のフラグ control_flag = True # 自粛宣言したか # エージェントシミュレーション for t in range(TIMELIMIT): T.append(t) xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD = calcn(agentsA) # 次時刻の状態を計算 im = [] # 左側グラフ（対策なしの表示 # subplot0：散布図 im += scatter_plot(im, 0, xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD) # subplot2：推移図 statasS_sum_left.append(len(xlistS)) statasI_sum_left.append(len(xlistI)) statasR_sum_left.append(len(xlistR)) statasD_sum_left.append(len(xlistD)) im += ax[2].stackplot(T, statasI_sum_left, statasR_sum_left, statasS_sum_left, statasD_sum_left, colors=["r","g", "b", "k"], alpha=0.7) # 右側グラフ（対策あり）の表示 xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD = calcn(agentsB) # 次時刻の状態を計算 if REQUEST_NOT_TO_GO_OUTSIDE_F and control_flag and statasI_sum2[t]>OVER_CAPACITY: # もし感染者の累計が全体のN/4を超えたら自粛要請が出る control_flag = False listS = [agentS for agentS in agentsB if agentS.state == "S"] for agent in random.sample(listS,int(CONTROL_RATE_AFTER*len(listS))): agent.control_f = 0 # 自粛状態になる # subplot1：散布図 im += scatter_plot(im, 1, xlistS, ylistS, xlistI, ylistI, xlistR, ylistR, xlistD, ylistD) # subplot3：推移図 statasS_sum_right.append(len(xlistS)) statasI_sum_right.append(len(xlistI)) statasR_sum_right.append(len(xlistR)) statasD_sum_right.append(len(xlistD)) im += ax[3].stackplot(T, statasI_sum_right, statasR_sum_right, statasS_sum_right, statasD_sum_right, colors=["r","g", "b", "k"], alpha=0.7) #描画設定 if legend_flag: # 一回のみ凡例を描画 ax[0].legend(loc='lower center', bbox_to_anchor=(1.1, 1.1), ncol=4) ax[0].set_xlim(0, SIZE) ax[0].set_ylim(0, SIZE) ax[0].tick_params(labelbottom=False,labelleft=False,labelright=False,labeltop=False, length=0) ax[0].tick_params(length=0) ax[0].set_title("No Measures") ax[1].set_xlim(0, SIZE) ax[1].set_ylim(0, SIZE) ax[1].tick_params(labelbottom=False,labelleft=False,labelright=False,labeltop=False, length=0) ax[1].tick_params(length=0) ax[1].set_title("80% stay") ax[2].tick_params(labelbottom=False,labelleft=True,labelright=False,labeltop=False) ax[2].axhline(OVER_CAPACITY, ls = "--", color = "black") ax[3].tick_params(labelbottom=False,labelleft=True,labelright=False,labeltop=False) ax[3].axhline(OVER_CAPACITY, ls = "--", color = "black") legend_flag = False ims.append(im) ani = animation.ArtistAnimation(fig, ims, interval=70) rc('animation', html='jshtml') ani
