分類問題の予測結果の評価指標（Accuracy, Precision, Recall, F値, AUC）について整理してみた

こんにちは。レッジインターン生の大熊です。今回は分類問題のタスクにおける予測結果の評価指標について、代表的なものをピックアップして書いていきます。評価指標は各タスクに合わせて設定しなければならず、またその評価値の閾値も個別に設定することが多いです。本記事を評価指標の選定の参考にしていただければ幸いです。

分類問題における正解・不正解のパターン

分類問題における実測値と予測値の関係性は以下のマトリクスで表現できます。

	正（実測）	負（実測）
正（予測）	TP	FP
負（予測）	FN	TN

TP：True Positive。実測値と予測値の両方が正であったもの。
FP：False Positive。実測値が負なのに、誤って正と予測値したもの（誤検知、偽陽性）。
TN：True Negative。実測値と予測値の両方が負であったもの。
FN：False Negative。実測値が正なのに、誤って負と予測値したもの（偽陰性）。

この内どの数値を用いるかが評価指標を見るときのポイントになります。

なぜAccuracy（正解率・ACC）だけでは不十分なのか？

Accuracyは「予測がどれだけ正しかったか」を見る指標です。以下のような式で表されます。

${\displaystyle\frac{TP + TN}{TP + TN + FP + FN}}$

噛み砕くと以下のようになります。

${\displaystyle\frac{予測が正しかった数}{予測したデータ数}}$

Accuracyは直感的に理解しやすく解釈もしやすいため、よく用いられている指標です。

しかし、Accuracyだけで予測結果を評価してしまうと、場合によっては良くないモデルを誤って良いモデルだと判断してしまう危険性があります。

Accuracyだけでは不均衡データで漏れが生じる

以下の例を考えてみましょう。

正負を当てる分類の問題で、100個のデータのうち2個が正、98個が負であったとします。

そしてこのとき、分類するモデルが「このデータは100個全てが負だ」と予測したとします。

すると、100個のデータのうち98個がもともと負なので、正解率は98％となります。数値（Accuraucy）だけを見ると結構良い数値に見えますよね。

しかし、正であったデータに関しては分類モデルは1つも予測できていません。これでは分類精度が高いとはゆめゆめ言えないのではないでしょうか。

上記のようにデータに不均衡が生じている場合、「すべて負だ」と予測してしまえば、たとえ正のデータが複数存在していたとしてもAccuracyの値は高くなってしまいます。

こうした問題を対処するために、以下のPrecisionやRecall、F値という指標を参照します。

Precision（適合率）：無駄打ちをなくすのが目標

Precisionは「正と予測したものが、どれだけ正しかったか」を見る指標です。 以下のような式で表されます。

${\displaystyle\frac{TP}{TP + FP}}$

噛み砕くと以下のようになります。

${\displaystyle\frac{正と予測した中で実際に正であったものの数}{正と予測したものの数}}$

Precisionでは、正と予測したものの正確性を見ることができます。そのためレコメンド等を行う場合、Precisionが高いほど無駄打ちをなくすことができます。

しかしPrecisonはFN（実際には正だったけど、誤って負と予測してしまったもの）を考慮しておらず、抜け漏れがあっても高い数値を返してしまいます。

この欠点を補完する性質を持つのが以下のRecallになります。

Recall（再現率）：機会損失をなくすのが目標

Recallは「実際に正であったもののうち、どれだけ正と予測できたか」を見る指標です。 以下のような式で表されます。

${\displaystyle\frac{TP}{TP + FN}}$

噛み砕くと以下のようになります。

${\displaystyle\frac{実際に正であったものの中で正と予測できた数}{実際に正であったものの数}}$

Recallは正の実測値をどれだけ網羅的に予測できたかを測ります。そのため、Recallを上げるということは、正であったもの全体を特定したいというモチベーションから、機会損失をなくしたい場合に向いている指標です。例えばがん検診のケースであれば、「ガンである人をガンでないと誤って予測する」ことは最も避けたいため、Recallを重視するのが良い例です。

RecallはPrecisionとトレードオフな関係にあります。トレードオフな関係とは、片方の値が高くなると、もう片方の値が低くなりやすいということです。どちらの値を重視するかはそれぞれの性質と分析の目的に合わせて設定するほか、特別こだわりがない場合には以下のF値を使用することが多いです。

F1, F0.5, F2：PrecisionとRecallの調和平均

PrecisionとRecallは両者補完的な性質を持つものでした。それら両方の値を考慮して予測結果の評価をしたものがF値になります。

F値はPrecisionとRecallの調和平均です。式は以下のように表されます。

F1： ${\displaystyle\frac{2Precision×Recall}{Precision + Recall}}$
F0.5（適合率重視）： ${\displaystyle\frac{1.25Precision×Recall}{0.25Precision + Recall}}$
F2（再現率重視）： ${\displaystyle\frac{5Precision×Recall}{4Precision + Recall}}$

F値はPrecisionとRecallのどれを重視したいかで算出方法が少し異なります。例えば品切れになりそうな商品を予測したい場合、「品切れになりそうなものをならないと予測する（偽陰性）」よりも「品切れにならないものを品切れと誤検知する（偽陽性）」ほうが在庫リスクの観点から避けるべきかもしれません。そうした場合はF0.5を採用したほうがよりリスクを抑えられたモデルの作成が行えると考えられます。

Fが高いというのはPrecisionとRecallがバランス良く高い値となっていることを表しています。その一方でPrecisionとRecallの片方が高くとも片方が著しく小さいとF値は小さい値を示します。

AUC：分類の閾値を変動させて評価

最後に紹介する評価指標がAUC(Area Under the Curve)です。名前の通り、ある曲線の下側の面積をモデルの評価指標とする指標です。

今まで紹介した評価指標とAUCの大きな違いは、AUCでは事前に分類の閾値を決めずに、閾値をずらしながら分類予測がどう変化していくかを見ることでモデルの評価を行う点にあります。ここでは2種類のAUCについて解説します。

➀ROC-AUC：ROC曲線を用いたAUC

ROC曲線はTPR(True Positive Rate)を縦軸、FPR(False Positive Rate)を横軸にとって描画されます。なお、TPRはRecallと同じです。FPRは「本来負であるもののうち、誤って正であると予測されたものの割合」を表し、以下のようにして求められます。

${\displaystyle\frac{FP}{FP + TN}}$

ROCは分類モデルが算出した予測確率値に対し様々な閾値を適用し、その時々のTRRとFPRの値をプロットすることで以下のように描画されます。TPRは高く、FPRは低い方が良いことを踏まえると、良いモデルというのは曲線が左上に引きあがったモデル、つまりAUCが大きくなるようなモデルが望ましいことがわかります。

➁PR-AUC：PR(Precison-Recall)曲線を用いたAUC

PR曲線はPrecisionを縦軸、Recallを横軸にとって以下のように描画されます。PrecisionとRecallの両方が高い状態が望ましことを踏まえると、良いモデルは曲線が右上に引きあがったモデルであり、ROC-AUCと同様AUCが高いモデルが望ましいことがわかります。

ROC曲線とPR曲線の使い所としては、不均衡データの分類の場合はPR曲線、それ以外はROC曲線のほうが良いと言われます。理論的な背景はこちらの論文が参考になります。

ロジスティック回帰で実験してみる

人工的にデータを作成して、実際に2種類のモデルを作成し、上記の評価指標を見てみます。必要なパッケージ等は以下です。

# データ作成&モデル構築用
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import SMOTE
from sklearn.linear_model import LogisticRegression

# 評価指標の算出
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import roc_curve, auc, precision_recall_curve

# 描画用
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

まずデータを作成します。データはscikit-learnのmake_classification()を用いることで生成できます。今回は10000個のサンプルを用意して2クラスの割合を99:1、特徴量を6つに設定したデータを以下のようにして生成します。

dat = make_classification(n_samples=10000, n_features=6,  n_classes=2, weights = [0.99, 0.01], random_state=123)
X = dat[0] # 説明変数
y = dat[1] # 目的変数

次にデータを学習用データとテストデータに8:2の割合で分割します。ここで、今回の2種類のモデルは以下のようにするため、分割データを2種類作ります。

学習データをそのまま学習させたモデル
正例ラベルをオーバーサンプリング*1して学習させたモデル

# 学習用とテスト用データの分割
# 80%を学習、20%をテストに利用する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)

#テストデータをオーバーサンプリングする
smote = SMOTE(ratio={0:X_train.shape[0], 1:X_train.shape[0]//9}, random_state=123)
X_train_resampled, y_train_resampled = smote.fit_sample(X_train, y_train)

データを作成できたので、モデルを作成します。

# モデルの設定
clf_org = LogisticRegression()
clf_smote = LogisticRegression()

# 学習
clf_org.fit(X_train, y_train)
clf_smote.fit(X_train_resampled, y_train_resampled)

モデル及び予測値が算出されたので、各モデルの評価を見てみます。まず各モデルにおける正解と予測の組み合わせをカウントした混同行列を確認します。

# 混同行列の可視化メソッドの作成
def plot_confusion_matrix(X, y, model, cutoff, title='confusion matrix', figsize=(10,8)):
    """
    混同行列を可視化する
    """
    def get_confusion_matrix(X, y, model, cutoff):
        """
        混同行列を取得する
        """
        cm = confusion_matrix(y, (model.predict_proba(X)[:, 1] >= cutoff))
        return cm

    fig = plt.figure(figsize=figsize)
    # 混同行列をヒートマップで可視化
    ax = fig.add_subplot(111)
    cm = get_confusion_matrix(X, y, model, cutoff)
    sns.heatmap(cm, annot=True, cmap='Blues', ax=ax, fmt='d')
    ax.set_title(title)

# モデル①の混同行列
plot_confusion_matrix(X=X_test, y=y_test, model=clf_org, cutoff=0.5, title='confusion matrix (model1)', figsize=(10,8))

# モデル➁の混同行列
plot_confusion_matrix(X=X_test, y=y_test, model=clf_smote, cutoff=0.5, title='confusion matrix (model2)', figsize=(10,8))

以下の図が描画されます。

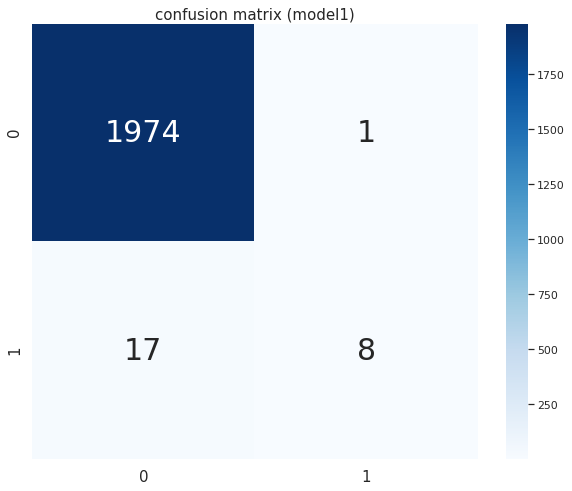
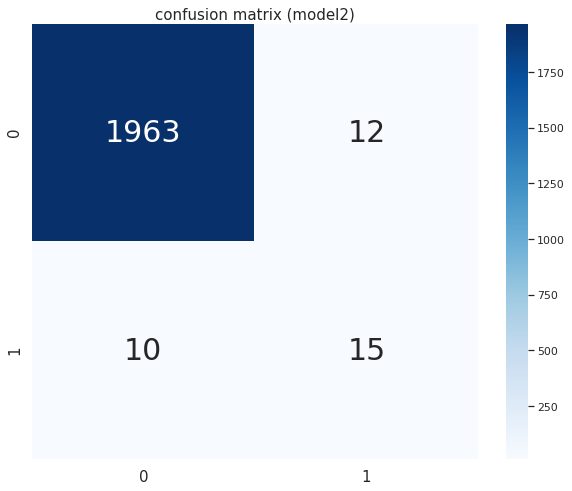
次にテストデータをそのまま学習させたモデルの評価指標を確認すると、以下のようになりました。

# 評価指標算出メソッドの作成
def print_metrics_by_cutoff(X, y, model, cutoff):
    """
    指定した閾値に基づくAccuracy, Precision, Recall, F1-scoreを出力する
    """
    y_pred = model.predict_proba(X)[:, 1] >= cutoff
    print('accuracy = {:.2f}'.format(accuracy_score(y_true=y, y_pred=y_pred)))
    print('precision = {:.2f}'.format(precision_score(y_true=y, y_pred=y_pred)))
    print('recall = {:.2f}'.format(recall_score(y_true=y, y_pred=y_pred)))
    print('f1 score = {:.2f}'.format(f1_score(y_true=y, y_pred=y_pred)))

def print_auc(X, y, model):
    """
    ROC, PR curveのAUCを出力する
    """
    scores = model.predict_proba(X)[:, 1]
    # ROC-AUC
    fpr_org, tpr_org, thresholds_org = roc_curve(y_true=y, y_score=scores)
    print('ROC-AUC = {:.2f}'.format(auc(fpr_org, tpr_org)))
    # PR-AUC
    precision_org, recall_org, thresholds = precision_recall_curve(y_test, scores)
    print('PR-AUC = {:.2f}'.format(auc(recall_org, precision_org)))

# モデル①
# Accuracy, Precision, Recall, F1-score
print_metrics_by_cutoff(X=X_test, y=y_test, model=clf_org, cutoff=0.5)

# AUC
print_auc(X=X_test, y=y_test, model=clf_org)

# accuracy = 0.99
# precision = 0.89
# recall = 0.32
# f1 score = 0.47
# ROC-AUC = 0.82
# PR-AUC = 0.54

次に学習データをオーバーサンプリングして作成したモデルは以下のようになりました。

# モデル②
# Accuracy, Precision, Recall, F1-score
print_metrics_by_cutoff(X=X_test, y=y_test, model=clf_smote, cutoff=0.5)

# AUC
print_auc(X=X_test, y=y_test, model=clf_smote)

# accuracy = 0.99
# precision = 0.56
# recall = 0.60
# f1 score = 0.58
# ROC-AUC = 0.82
# PR-AUC = 0.53

上記を表でまとめると以下のように比較できます。

評価指標	モデル①	モデル②
Accuracy	0.99	0.99
Precision	0.89	0.56
Recall	0.32	0.60
F1 score	0.47	0.58
ROC-AUC	0.82	0.82
PR-AUC	0.54	0.53

また、各ROC曲線は以下のように描画されます。

# ROC
def plot_roc_curve(X, y, models: list, labels: list, figsize=(6.4, 4.8)):
    """
    ROC曲線をプロットする
    """
    fig = plt.figure(figsize=figsize)
    ax = fig.add_subplot(111)

    for model, label in zip(models, labels):
        scores = model.predict_proba(X)[:, 1]
        fpr_org, tpr_org, thresholds_org = roc_curve(y_true=y, y_score=scores)
        ax.plot(fpr_org, tpr_org, label=label)

    ax.plot([0, 1], [0, 1], linestyle='--', label='random')
    ax.plot([0, 0, 1], [0, 1, 1], linestyle='--', label='ideal')
    ax.legend()
    ax.set_title('ROC curve')
    ax.set_xlabel('false positive rate')
    ax.set_ylabel('true positive rate')
    plt.show()

models = [clf_org, clf_smote]
labels = ['roc curve (model1)', 'roc curve (model2)']

plot_roc_curve(X=X_test, y=y_test, models=models, labels=labels)

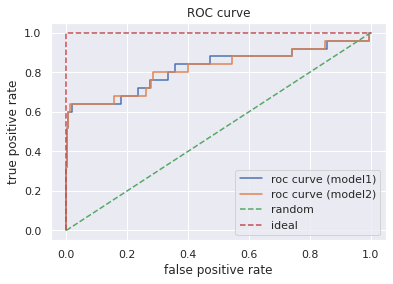
次に各PC曲線は以下のように描画されます。

# PR
def plot_pr_curve(X, y, models: list, labels: list, figsize=(6.4, 4.8)):
    """
    PR曲線をプロットする
    """
    fig = plt.figure(figsize=figsize)
    ax = fig.add_subplot(111)

    for model, label in zip(models, labels):
        scores = model.predict_proba(X)[:, 1]
        precision_org, recall_org, thresholds = precision_recall_curve(y_test, scores)
        ax.plot(recall_org, precision_org, label=label)

    ax.legend()
    ax.set_title('PR curve')
    ax.set_xlabel('Recall')
    ax.set_ylabel('Precision')
    plt.show()

models = [clf_org, clf_smote]
labels = ['pr curve (model1)', 'pr curve (model2)']

plot_pr_curve(X=X_test, y=y_test, models=models, labels=labels)

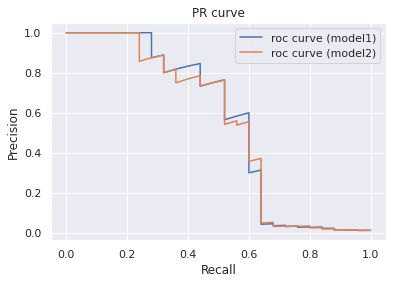
2つのモデルを比較すると、AccuracyとAUCは同程度です。しかしモデル①では、Precisionは高いがRecallが低いアンバランスな結果となっています。その一方でモデル②では、Precisionはモデル①より低いもののRecallの値が改善され、PrecisionとRecallのバランスが取れている結果となっています。その結果、モデル①よりもモデル②のほうがF1値が高くなっています。ゆえに、PrecisionとRecallを同程度に重視したい場合はサンプリングを工夫したモデル②のほうが良い評価を得られていると解釈できます。

またROC-AUCとPR-AUCを比較すると、後者のほうがモデルを低く評価している事がわかります。