こんにちは。レッジのインターン生の大熊です。前回のマルチエージェントの記事に続き、今回が2回目の投稿です。

本稿では傾向スコアを使用して因果効果を推定する方法の1つである、二重にロバスト（DR：Doubly Robust）な推定法をPythonで実装していきます。

DR推定には大きく分けて2つのステップがあります。1つが傾向スコアの算出です。もう1つは介入があった/なかったグループにおいてそれぞれ回帰分析を行うことです。本稿ではまずこの傾向スコアを概説します。そしてDR推定のもととなるIPW推定法を説明したのち、DR推定を実装します。

なお本稿は以下の3つの書籍を参照して記述しています。本稿で紹介していない理論的な枠組みを知りたい方にとって、特に3つ目の書籍は大変参考になります。

また、コードはこちらの記事を参考にしています。

傾向スコアとは

傾向スコアとは、各サンプルが介入を受ける確率のことです。傾向スコアは確率値なので、各サンプルに対して0から1の実数値をとります。

この傾向スコアはロジスティック回帰などを用いて、各サンプルの持つ観測された共変量を説明変数、介入の有無（0 or 1）を目的変数に置くことで求めることができます。ポイントは、共変量から介入の有無を確率的に説明するところです。

また傾向スコアを使用する利点として、介入変数に対するモデリングを行えばよく、目的変数に対するモデリングが不要な点が挙げられます。

効果検証の手法として傾向スコアとよく対比されるのが、回帰分析による手法です。回帰分析による手法では共変量の選定や調整、そしてその解釈が困難な場合が少なくありません。傾向スコアを使用した解析ではこのような煩雑な作業を軽減して効果量を推定することができます。（その一方で傾向スコアを適用できる条件として、「強く無視できる割当：どちらのグループに割付られるかは観測された共変量の値に依存し，従属変数の値に依存しない」というのもあります。詳しくはこちらをご参照ください。）

傾向スコアによる逆確率重みづけ法（IPW：Inverse Probability Weighting）について

DR推定法を説明する前に、IPWを理解しておく必要があります。なぜならDR推定法は、IPW推定法を拡大したものだからです。

IPWによる推定法とは、サンプルを傾向スコアの逆数で重みづけすることで、共変量によるバイアスを調整する方法です。IPWで調整された目的変数の期待値の差、すなわちIPWE（Inverse Probability Weighting Estimator）を以下に式として示します。

なお本稿で紹介しているのは平均処置効果（ATE：Average Treatment Effect）です。処置群における平均処置効果（ATT：Average Treatment Effect on the Treated）や対照群における平均処置効果（ATU：Average Treatment Effect on the Untreated）を算出する場合は重みづけの対象が異なります。

まず、介入を受けた群におけるIPW推定量は以下となります。

$\hat{E}(y_1) = \left [ \sum_{i=1}^{n} \frac{z_iy_{i1}}{e(x_i)} \right ] / \left [ \sum_{i=1}^{n} \frac{z_i}{e(x_i)} \right ]$

その一方、介入を受けていない群におけるIPW推定量は以下となります。

$\hat{E}(y_0) = \left [ \sum_{i=1}^{n} \frac{(1-z_i)y_{i1}}{1-e(x_i)} \right ] / \left [ \sum_{i=1}^{n} \frac{1-z_i}{1-e(x_i)} \right ]$

この差分が因果効果を表します。 $n$ 個のサンプルのうち1~ $J$ までのサンプルに介入が行われていた場合、上記の式に用いられている変数は以下のように定義されます。

$z_i=\left\{\begin{matrix} 1~~~~~z=j \\ 0~~~~~z\neq j \end{matrix}\right. (j = 1,\cdots,J)$

$y_{i1}, y_{i0}$ ：サンプル $i$ において観測された目的変数（下付きの数字は介入の有無を表しており、 $z_i$ の値に対応している）

$x_i$ ：サンプル $i$ における共変量ベクトル

$e(x_i)$ ：サンプル $i$ における傾向スコア

この式で定義されるIPWは、以下の2つの観点から改善の余地が残されています。

IPWの推定量には対照群（介入を受けていない群）の共変量の情報を利用していない点
傾向スコアを算出するモデルの精度が低い場合、傾向スコアを用いた解析法は誤った結果を与える可能性がある点

こうした改善点を補うのが、次で紹介する本稿のメインとなるDR推定法です。

二重にロバストな推定法とは

DR推定法では、介入確率を共変量で説明する回帰モデル、つまり傾向スコアを算出するモデルのほかに、目的変数を共変量で説明する回帰モデルを使用します。このどちらかが正しく成立していれば因果効果を正しく説明できる（一致推定量を得る）ことがわかっています。

具体的に、介入を受けた群における目的変数の二重にロバストな推定量は以下となります。

$\hat{E^{DR}}(y_1) = \frac{1}{n}\sum_{i=1}^{n}\left [ \frac{z_i}{e(x_i)}y_{i1}+\left ( 1- \frac{z_i}{e(x_i)}\right )\hat{y_{i1}} \right ]$

同様に介入を受けていない群における目的変数の二重にロバストな推定量は以下となります。

$\hat{E^{DR}}(y_0) = \frac{1}{n}\sum_{i=1}^{n}\left [ \frac{1-z_i}{1-e(x_i)}y_{i0}+\left ( 1- \frac{1-z_i}{1-e(x_i)}\hat{y_{i0}}\right ) \right ]$

これらの差分を取ることで、因果効果の推定量を算出できます。

IPWの式と比較してDR推定量では、 $\hat{y_{i1}}$ と $\hat{y_{i0}}$ として目的変数を共変量で説明する回帰モデルが含まれています。すなわち、 $\hat{y_{i1}}$ と $\hat{y_{i0}}$ はそれぞれ以下の回帰モデルによるサンプル $i$ の目的変数の予測値です。

$z_i=1$ における共変量で ${y_{i1}}$ を説明する回帰モデル
$z_i=0$ における共変量で ${y_{i0}}$ を説明する回帰モデル

それではこのDR推定法を利用して、実際に因果効果を推定していきます。

PythonでDR推定量を出す

この章では、Pythonでサンプルデータをもとに、実際にDR推定量を算出します。

今回はLaLonde（1986）のデータセットを使用します。これはThe National Supported Work Demonstration (NSW)という職業訓練プログラムの効果を評価する際に使用されたデータです。論文の説明はこちらが参考になります。

本稿ではまず、RCTで得られたデータを回帰分析して介入効果の推定値を見ます。次にバイアスを付与したデータに対してDR推定量を算出します。そして最後にRCTデータにおける推定値とDR推定量を比較検討します。

環境

Jupyter Notebook上で以下の環境で実装しています。

python == 3.6
pandas == 1.0.5
numpy == 1.18.5
sklearn == 0.0
statsmodels == 0.10.2
matplotlib == 3.2.2

パッケージとデータの読み込み

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
import statsmodels.api as sm
import matplotlib.pyplot as plt
import random
import warnings
warnings.filterwarnings('ignore')

バイアスのあるデータを生成します。データはそれぞれ以下のように表されます。

# RCTのデータ
nswdw_data = pd.read_stata('https://users.nber.org/~rdehejia/data/nsw_dw.dta')
# バイアスを付与したデータ（cps1_nsw_data）の生成
cps1_data = pd.read_stata('https://users.nber.org/~rdehejia/data/cps_controls.dta')
cps1_nsw_data = pd.concat([nswdw_data[nswdw_data["treat"] == 1], cps1_data], ignore_index=True)

RCTデータにおける介入効果の確認

# 共変量付きの回帰分析
# 目的変数
y = nswdw_data.re78
# 説明変数
X = nswdw_data[['treat', 're74', 're75', 'age', 'education', 'black', 'hispanic', 'nodegree', 'married']]
# y切片の追加
X = sm.add_constant(X)
# モデル作成
results = sm.OLS(y, X).fit()
# 結果表示
results.summary().tables[1]

	coef	std err	t	P>\|t\|	[0.025	0.975]
const	785.0614	3374.969	0.233	0.816	-5848.211	7418.334
treat	1676.3426	638.682	2.625	0.009	421.056	2931.629
re74	0.0821	0.077	1.061	0.289	-0.070	0.234
re75	0.0528	0.135	0.389	0.697	-0.214	0.319
age	55.3167	45.284	1.222	0.223	-33.686	144.319
education	395.7343	227.415	1.740	0.083	-51.234	842.703
black	-2159.5222	1169.036	-1.847	0.065	-4457.183	138.139
hispanic	164.0327	1549.457	0.106	0.916	-2881.320	3209.386
nodegree	-70.6806	1004.387	-0.070	0.944	-2044.736	1903.374
married	-138.7253	879.728	-0.158	0.875	-1867.771	1590.321

treat行の一列目を確認すると、1676.34...とあります。そのため、バイアスのあるデータをDR推定法使って調整するとき、結果としての効果量をこの1676付近に近づければいいということになります。

DR推定量の算出

それでは、前の章の式の通りに計算を行います。

初めにcps1_nsw_dataで確認をします。

# DR推定量の取得を関数化
def get_dr(df, y_column, x_columns, treat_column, dummy_columns=[]):
    """
    DR推定量を算出する関数

    Parameters:
    ----------
    df : dataframe
        目的変数、共変量、介入有無のフラグ、傾向スコアのカラムが入ったデータフレーム
    y_column : str
        目的変数のカラム名
    x_columns : list
        説明変数のカラム名が格納されているリスト
    treat_column : str
        介入有無のフラグがあるカラム名
    dummy_columns : list
        説明変数うち、ダミー変数にする必要のあるカラム名が格納されているリスト

    Returns:
    ----------
    result : int
    """
    ## DR推定量の算出
    n = len(df)
    # 結果変数
    y = df[y_column]
    #共変量
    X = pd.get_dummies(df[x_columns], columns=dummy_columns, drop_first=True)
    # 介入効果
    z = df[treat_column]
   # 傾向スコアの算出
    ps_model = LogisticRegression(solver="lbfgs", random_state=1).fit(X, z)
    ps_score = ps_model.predict_proba(X)[:, 1]
    # 介入群のみのデータ
    group1_df = df[df[treat_column]==1]
    y1 = group1_df[y_column]
    X1 = pd.get_dummies(group1_df[x_columns], columns=dummy_columns, drop_first=True)
    # 対照群のみのデータ
    group0_df = df[df[treat_column]==0]
    y0 = group0_df[y_column]
    X0 = pd.get_dummies(group0_df[x_columns], columns=dummy_columns, drop_first=True)
    # 介入群に対するモデル
    model1 = sm.OLS(y1, X1).fit()
    # 対照群に対するモデル
    model0 = sm.OLS(y0, X0).fit()
    # データ全体をpredictする
    fitted1 = model1.predict(X)
    fitted0 = model0.predict(X)
    # 推定
    dre1 = sum(z * y / ps_score + (1 - z  / ps_score)* fitted1) / n
    dre0 = sum((1 - z) /(1 - ps_score) * y + (1 - (1 - z)  / (1 - ps_score))* fitted0) / n


    result = dre1 - dre0
    return result

y_column = "re78"
x_columns =['age', 'education', 'black', 'hispanic', 'nodegree', 'married', 're74', 're75']
treat_column = "treat"
result = get_dr(cps1_nsw_data, y_column, x_columns, treat_column)
result

> result
-4629.225071849434

1600付近からかなり遠のいてしまいました。そこで、傾向スコアの分布を確認してみます。

# 傾向スコアのヒストグラム
plt.hist(ps_score, bins=10, label="10 bins")
plt.hist(ps_score, bins=100, label="100 bins")
plt.title("Distribution of the Ps Score")

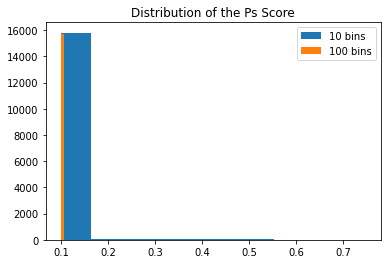
かなり小さい傾向スコアを持つサンプルがたくさん存在していました。どうやらこれが原因のようです。

IPW推定量と同様にDR推定量も傾向スコアの逆数で重みづけがされています。傾向スコアが極端に小さい値があるとゼロ徐算のような計算が含まれるために推定の分散が大きくなり、その結果、効果の推定に予期しない影響を与えることになります。

小さい傾向スコアをトリミングしてDR推定量を算出

上記のような問題に対処する方法として、傾向スコアを一定の値でトリミングする方法があります。そこで今回は、トリミングレベルを1％, 5%, 10%の3種類として、DR推定量の再計算を行います。

結果は以下の通りでした。

トリミングレベル1％：-3573.8529339209617
トリミングレベル5％：-3630.857794205538
トリミングレベル10％：-3639.0593447037772

若干のトリミングはバイアスの軽減につながるが、一定以上のウェイトをトリミングするとバイアスが大きくなることがわかります。この結果はLee(2011)の結果と整合性が取れています。そのためトリミングを行う方法は、今回の検証においては根本的な解決には至らないということがわかります。

(補足)

上記の内容ではDR推定法に有用性がないように見えてしまいそうなので、違うデータセットでの結果を用いて補足説明をします。

上記とは別に、『効果検証入門』で作成されているバイアスのあるデータ（メールマーケティングデータ）を使用します。このデータは、Mine ThatData E-Mail Analytics And Data Mining Challenge dataset というRTCによって得られたデータセットを元にして、顧客に最後の購入からの経過月数、昨年の購入額、使用チャネルの種類によってバイアスを付与したデータです。

まず、RTCデータを用意します。『効果検証入門』では「男性向けメールの配信の有無」がコンバージョン率や購買金額に影響を与えているか見ることを目的にしているので、以下のように整形されます。

# データの読み込み
male_df = pd.read_csv("http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv")
#　女性向けメールが配信されたデータを削除
male_df = male_df[male_df["segment"] != "Womens E-Mail"].copy()
# 介入を表すtreatment作成
male_df["treatment"] = male_df["segment"].apply(lambda x : 1 if x == "Mens E-Mail" else 0)

# バイアスを付与
sample_rules = (male_df['history'] > 300) | (male_df['recency']<6) | (male_df['channel']=="Multichannel")
biased_df = pd.concat([
    male_df[(sample_rules)&(male_df.treatment==0)].sample(frac=0.5, random_state=1),
    male_df[(sample_rules)&(male_df.treatment==1)],
    male_df[(~sample_rules)&(male_df.treatment==0)],
    male_df[(~sample_rules)&(male_df.treatment==1)].sample(frac=0.5, random_state=1),
], axis=0, ignore_index=True)

RTCデータにおける購入金額の平均値は以下のようになります。

male_df.groupby('treatment').agg(
    spend_mean=('spend', 'mean'), # グループごとのspendの平均
    count=('treatment', 'count') # グループごとのデータ数
)

	spend_mean	count
treatment
0	0.652789	21306.0
1	1.422617	21307.0

これにより、メール配信の効果は1.42 - 0.65 = 0.77程度であることがわかりました。なお結果には問題ありませんが、データ作成の都合上、『効果検証入門』に掲載されている値とは異なります。

次に購入金額が高い、購買頻度が高い、接触チャネルが複数ある顧客に配信が多くなされるようなバイアスを付与します。

sample_rules = (male_df['history'] > 300) | (male_df['recency']<6) | (male_df['channel']=="Multichannel") # メールが多く配信されるグループのルール設定
biased_df = pd.concat([
    male_df[(sample_rules)&(male_df.treatment==0)].sample(frac=0.5, random_state=1), # sample_ruleの条件に当てはまっていながらもメールが配信されていないサンプルを半分にする
    male_df[(sample_rules)&(male_df.treatment==1)],
    male_df[(~sample_rules)&(male_df.treatment==0)],
    male_df[(~sample_rules)&(male_df.treatment==1)].sample(frac=0.5, random_state=1), # sample_ruleの条件に当てはまっていないのにメールが配信されているサンプルを半分にする
], axis=0, ignore_index=True)

バイアスのあるデータにおける購入金額の平均値は以下のようになります。

biased_df.groupby('treatment').agg(
    spend_mean=('spend', 'mean'), # グループごとのspendの平均
    count=('treatment', 'count') # グループごとのデータ数
)

	spend_mean	count
treatment
0	0.557954	14757.0
1	1.541704	17168.0

これによると、メール配信の効果は1.54 - 0.56 = 0.98です。RCTデータでは0.77であったことから、バイアスにより効果が歪んで出ていることがわかります。

それでは、これまでと同様にDR推定量を算出します。算出したところ、以下のような結果を確認できました。

> result
0.878432429179677

LaLondeのデータセットとは異なり、RTCデータに近い値が算出されました。このような結果から、傾向スコアを使用して因果効果を推定する場合、傾向スコアの分布および共変量がバランスされてることを確認したうえで、結果を解釈する必要があるとわかります。

まとめ

本稿では、DR推定量の実装とその検証を2種類のデータで行いました。2種類の回帰の精度に依存する手法であることから、「Doubly Robust」だからといって万能なわけではなく、その恩恵を受けるためには傾向スコアがどのように振られ、共変量がどのようにバランスしているか見定める必要があるとわかりました。現実的にはマッチングやIPW等の結果を加味して総合的に判断するのが良いと思われます。